HSNW
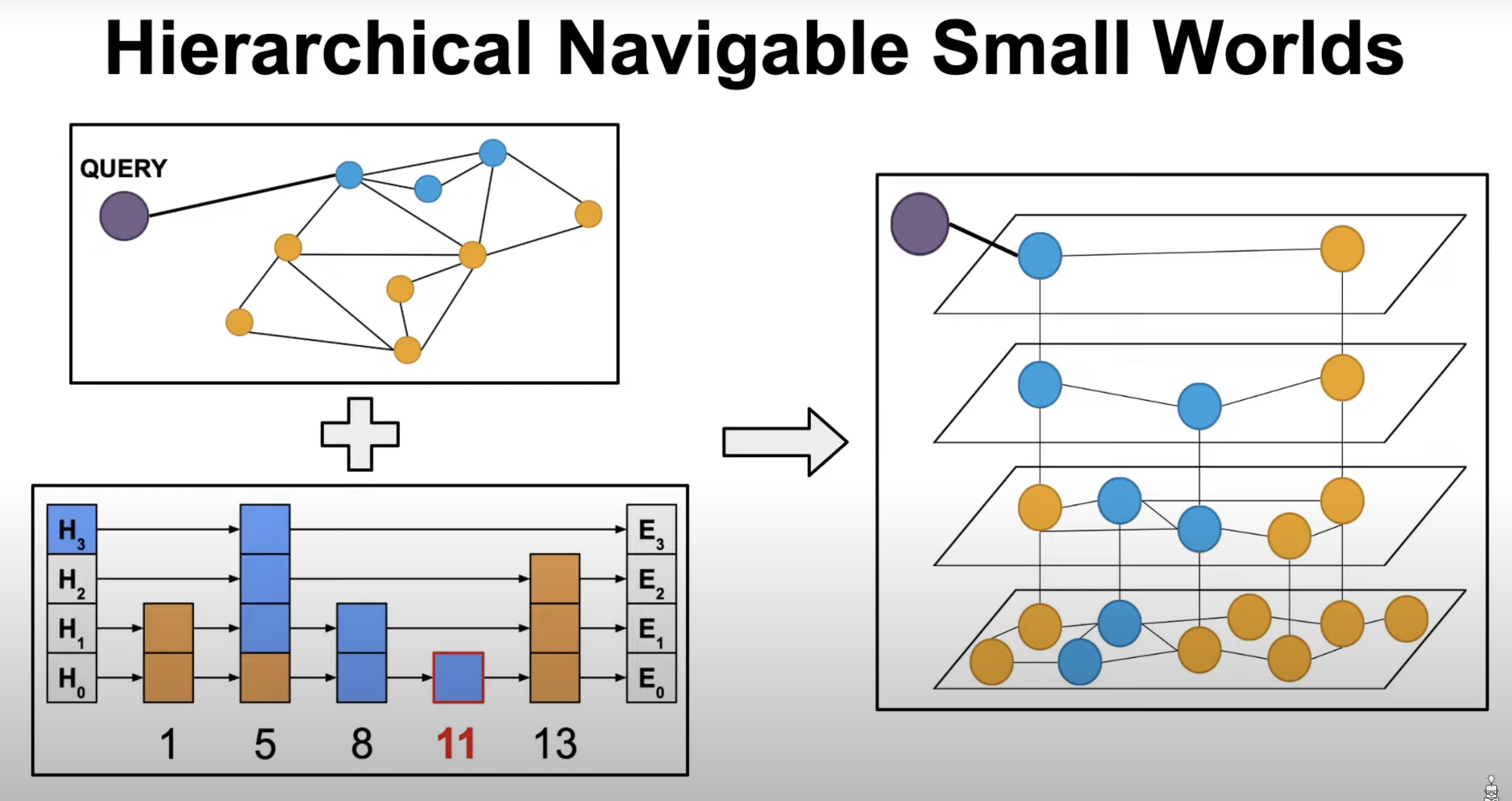
HSNW is a search algorithm that averages O(log N) as opposed to brute force which is O(N).
HSNW combines using both a graph and a skip list. And it works by having every layer below contain all nodes from the layer above. The algorithm of course has an accuracy hit in order to improve performance. It is an approximation method.
For example, if we don’t go down a layer, the algorithm misses finer-grained neighbors. Or if a node’s neighbors are all poor we miss to traverse further throughout a graph.
IVF_FLAT (Flat means)
IVF = Inverted File Index: a method that clusters the vector space into “buckets” (using k-means or similar) FLAT = brute-force exact search inside each selected cluster
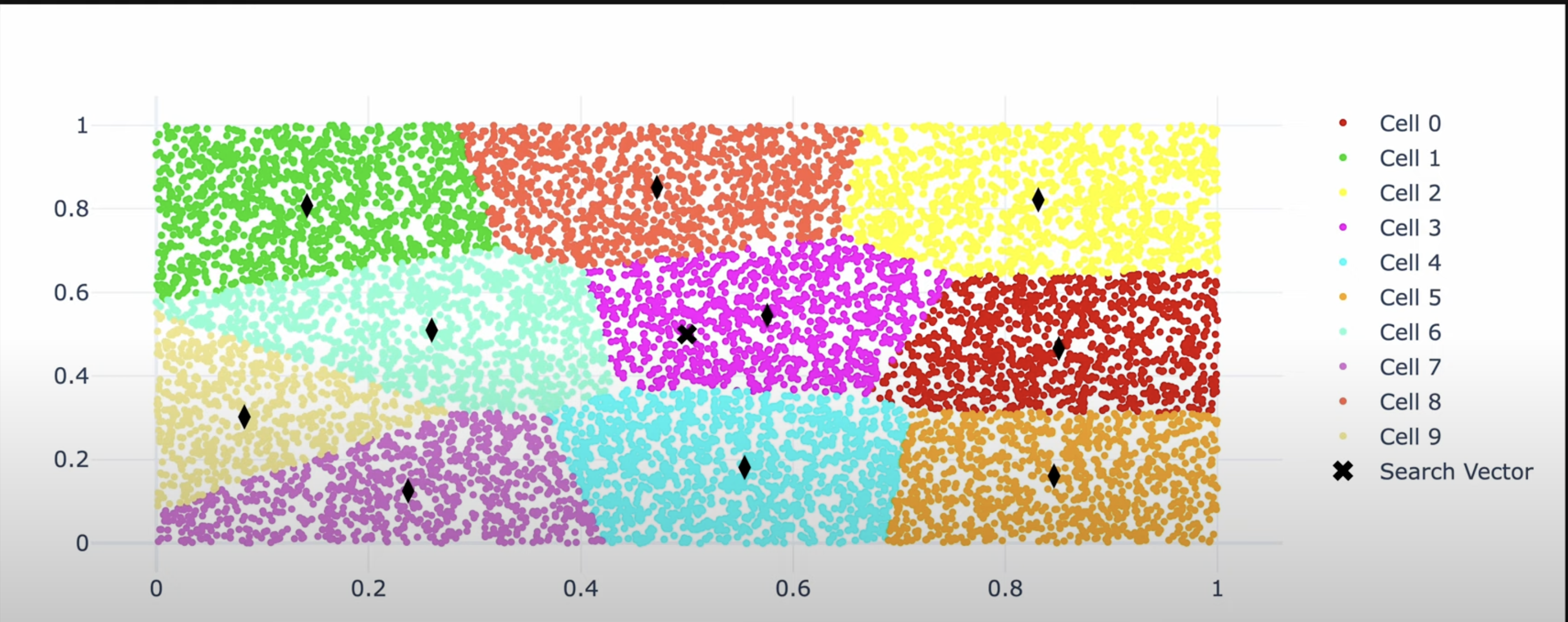
Index (Offline) In this technique we first build our index by specifying a cluster count. In this case 10. The algorithm goes ahead and computes 10 clusters using k-means.
Search (Online) For a new query vector:
- Find the top
nprobecentroids closest to the query. - For each of these clusters, do a brute-force (flat) search among all vectors in that cluster.
- From the union of these results, return the top-k closest vectors.
- Higher
nprobe→ searches more clusters → higher accuracy, slower - Lower
nprobe→ searches fewer clusters → faster, lower recall
K-means (refresher)
K-means is an algorithm for grouping n clusters. It works by picking random n centroids at first and then assigning each point to its closest centroid. Then the centroids are updated to the mean of all their points. Then the points are reassigned. Then the centroids are reassigned again. And this continues until stopping condition. Usually when the cluster centroids stop changing significantly between iterations.
Playful Visualization (https://www.naftaliharris.com/blog/visualizing-k-means-clustering)
Recall
Recall measures how many of the true (exact) nearest neighbors your algorithm actually finds Recall@k = (# of true nearest neighbors found in top-k results) / k So:
- If the exact nearest neighbors are
[A, B, C, D, E] - And your approximate search returns
[A, C, F, G, H]Then: - You found 2 out of 5 true neighbors ⇒ Recall@5 = 0.4
